943. В остроугольном треугольнике ABC
сторона AB
меньше стороны AC
, D
— точка пересечения прямой DB
, перпендикулярной к AB
, и прямой DC
, перпендикулярной к AC
. Прямая, проходящая через точку B
перпендикулярно к AD
, пересекает AC
в точке M
. Известно, что AM=m
, MC=n
. Найдите AB
.
Ответ. \sqrt{m(m+n)}
.
Указание. Докажите, что треугольники ABM
и ACB
подобны.
Решение. Поскольку \angle ABD=\angle ACD=90^{\circ}
, то точки A
, B
, D
и C
лежат на окружности с диаметром AD
. Поэтому
\angle ABM=90^{\circ}-\angle MBD=\angle BDA=\angle BCA.
Следовательно, треугольники ABM
и ACB
подобны по двум углам. Поэтому \frac{AM}{AB}=\frac{AB}{AC}
. Отсюда находим, что
AB^{2}=AM\cdot AC=m(m+n).
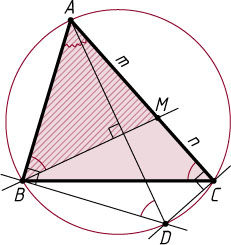
Источник: Вступительный экзамен на физический факультет МГУ. — 1991, № 4, вариант 2
