944. Две окружности разных радиусов касаются в точке C
одной и той же прямой и расположены по одну сторону от неё. Отрезок CD
— диаметр большей окружности. Из точки D
проведены две прямые, касающиеся меньшей окружности в точках A
и B
. Прямая, проходящая через точки C
и A
, образует с общей касательной к окружностям в точке C
угол 75^{\circ}
и пересекает большую окружность в точке M
. Известно, что AM=\sqrt{2-\sqrt{3}}
. Найдите площадь фигуры, ограниченной отрезками касательных DA
, DB
и дугой ACB
меньшей окружности.
Ответ. 2(5\pi+4\sqrt{3})
.
Указание. Составьте систему уравнений относительно радиусов данных окружностей.
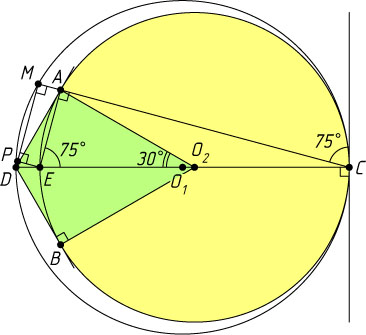
Решение. Пусть r
и R
— радиусы окружностей (r\lt R
), O_{2}
и O_{1}
— их центры, E
— вторая точка пересечения прямой CD
с меньшей окружностью, P
— проекция точки E
на MD
. По теореме об угле между касательной и хордой
\angle AEC=\angle MDC=75^{\circ}.
Поскольку \angle CAE=\angle CMD=90^{\circ}
, то AMPE
— прямоугольник. Поэтому
PE=MA=\sqrt{2-\sqrt{3}}=\frac{\sqrt{3}-1}{\sqrt{2}}.
Из прямоугольного треугольника EPD
находим, что PE=ED\sin75^{\circ}
, или
\frac{\sqrt{3}-1}{\sqrt{2}}=\frac{2(R-r)(\sqrt{3}+1)\sqrt{2}}{4}.
Поэтому R-r=2-\sqrt{3}
.
В прямоугольном треугольнике O_{2}AD
известно, что
AO_{2}=r,~O_{2}D=2R-r,~\angle AO_{2}D=2\angle ACO_{2}=30^{\circ}.
Поэтому r=\frac{(2R-r)\sqrt{3}}{2}
. Из полученной системы уравнений находим, что r=2\sqrt{3}
.
Искомая площадь равна сумме площадей сектора O_{2}ACB
\left(\frac{5\pi r^{2}}{6}\right)
и четырёхугольника O_{2}ADB
(O_{2}A\cdot AD
), т. е.
\frac{5\pi r^{2}}{6}+\frac{r^{2}}{\sqrt{3}}=2(5\pi+4\sqrt{3}).
Источник: Вступительный экзамен на химический факультет МГУ. — 1991, № 5, вариант 2
