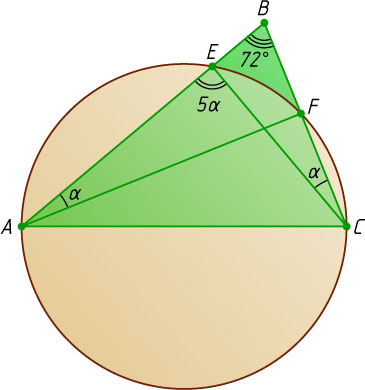
950. Окружность проходит через вершины A
и C
треугольника ABC
, пересекая сторону AB
в точке E
и сторону BC
в точке F
. Угол AEC
в 5 раз больше угла BAF
, а угол ABC
равен 72^{\circ}
. Найдите радиус окружности, если AC=6
.
Ответ. 3.
Решение. Обозначим \angle BAF=\alpha
. Тогда \angle AEC=5\alpha
. Вписанные углы ECF
и EAF
опираются на одну и ту же дугу, поэтому \angle BCE=\angle ECF=\angle EAF=\angle BAF=\alpha
.
По теореме о внешнем угле треугольника \angle ABC+\angle BCE=\angle AEC
, или 72^{\circ}+\alpha=5\alpha
, откуда находим, что \alpha=\frac{1}{4}\cdot72^{\circ}=18^{\circ}
, значит, \angle AEC=5\alpha=5\cdot18^{\circ}=90^{\circ}
.
Центр окружности, описанной около прямоугольного треугольника AEC
, — середина гипотенузы AC
, поэтому радиус окружности равен половине AC
, т. е. 3.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1991, № 5, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.6, с. 103
