951. В полукруг помещены две окружности диаметром d
и D
(d\lt D
) так, что каждая окружность касается дуги и диаметра полукруга, а также другой окружности. Через центры окружностей проведена прямая, пересекающая продолжение диаметра полукруга в точке M
. Из точки M
проведена касательная к дуге полукруга (N
— точка касания). Найдите MN
.
Ответ. \frac{Dd}{D-d}
.
Указание. Докажите, что прямая, проходящая через точки касания окружностей с данной полуокружностью проходит через точку M
. Затем примените теорему о касательной и секущей.
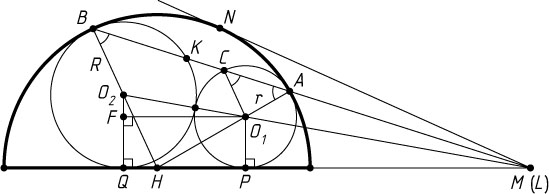
Решение. Пусть O_{1}
и O_{2}
— центры данных окружностей, r
и R
соответственно — радиусы (r\lt R
), A
и B
— точки касания с полуокружностью, C
и K
— точки пересечения прямой AB
с первой и второй окружностью соответственно, P
и Q
— точки касания с диаметром полуокружности, H
— центр полуокружности.
Поскольку треугольники AHB
, KO_{2}B
и AO_{1}C
— равнобедренные, то \angle ACO_{1}=\angle KBO_{2}
. Поэтому O_{1}C\parallel O_{2}B
.
Пусть L
— точка пересечения прямых AB
и O_{1}O_{2}
. Тогда
\frac{LO_{1}}{LO_{2}}=\frac{CO_{1}}{BO_{2}}=\frac{r}{R}.
Поэтому
\frac{LO_{1}}{O_{1}O_{2}}=\frac{r}{R-r}.
С другой стороны, так как O_{1}P\parallel O_{2}Q
, то
\frac{MO_{1}}{MO_{2}}=\frac{O_{1}P}{O_{2}Q}=\frac{r}{R}.
Поэтому
\frac{MO_{1}}{O_{1}O_{2}}=\frac{r}{R-r}=\frac{LO_{1}}{O_{1}O_{2}}.
Следовательно, точки L
и M
совпадают.
По теореме о касательной и секущей
MN^{2}=MB\cdot MA=\frac{R}{r}\cdot MC\cdot MA=\frac{R}{r}\cdot MP^{2}.
Пусть F
— проекция O_{1}
на O_{2}Q
. Из прямоугольного треугольника O_{1}FO_{2}
находим, что
O_{1}F=\sqrt{O_{1}O_{2}^{2}-O_{2}F^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{rR}.
Из подобия треугольников MPO_{1}
и O_{1}FO_{2}
следует, что \frac{MP}{O_{1}F}=\frac{O_{1}P}{O_{2}F}
. Отсюда находим, что
MP=\frac{O_{1}F\cdot O_{1}P}{O_{2}F}=\frac{2r\sqrt{rR}}{R-r}.
Следовательно,
MN^{2}=\frac{R}{r}\cdot\left(\frac{2r\sqrt{rR}}{R-r}\right)^{2}=\frac{4R^{2}r^{2}}{(R-r)^{2}},~MN=\frac{2rR}{R-r}=\frac{dD}{D-d}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1984, вариант 2, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 39
