954. Через вершины A
и B
треугольника ABC
проведена окружность радиуса 2\sqrt{5}
, отсекающая от прямой BC
отрезок, равный 4\sqrt{5}
, и касающаяся прямой AC
в точке A
. Из точки B
проведён перпендикуляр к прямой BC
до пересечения с прямой AC
в точке F
. Найдите площадь треугольника ABC
, если BF=2
.
Ответ. \frac{5\sqrt{5}}{3}
.
Указание. Докажите, что центр данной окружности лежит на прямой BC
и рассмотрите два возможных варианта расположения этого центра на BC
относительно точки B
.
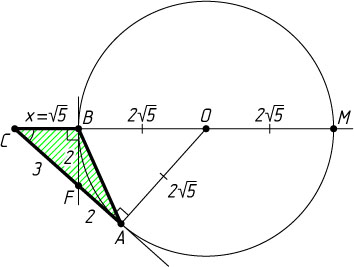
Решение. Пусть M
— отличная от B
точка пересечения данной окружности с прямой BC
. Поскольку BM=4\sqrt{5}
и диаметр окружности равен 4\sqrt{5}
, то BM
— диаметр окружности.
Пусть O
— центр этой окружности. Обозначим BC=x
. Предположим, что точка M
лежит между C
и B
. Тогда из подобия треугольников CAO
и CBF
следует, что \frac{AO}{BF}=\frac{CO}{CF}
, или
\frac{2\sqrt{5}}{2}=\frac{x-2\sqrt{5}}{\sqrt{x^{2}+4}},~\mbox{или}~4x^{2}+4x\sqrt{5}=0,
что невозможно, так как x\gt0
. Поэтому точка B
лежит между точками C
и M
. Тогда из подобия треугольников CAO
и CBF
имеем:
\frac{2\sqrt{5}}{2}=\frac{x+2\sqrt{5}}{\sqrt{x^{2}+4}}
Отсюда находим, что x=\sqrt{5}
. Тогда
AC=\sqrt{OC^{2}-OA^{2}}=\sqrt{(3\sqrt{5})^{2}-(2\sqrt{5})^{2}}=5,
\sin\angle ACB=\frac{BF}{CF}=\frac{2}{3},
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\sin\angle ACB=\frac{1}{2}\cdot5\cdot\sqrt{5}\cdot\frac{2}{3}=\frac{5\sqrt{5}}{3}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1987, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 103
