956. В прямоугольном треугольнике острый угол равен \alpha
, а радиус окружности, описанной около этого треугольника равен R
. Найдите высоту треугольника, опущенную на гипотенузу.
Ответ. R\sin2\alpha
.
Указание. Гипотенуза прямоугольного треугольника есть диаметр окружности, описанной около этого треугольника.
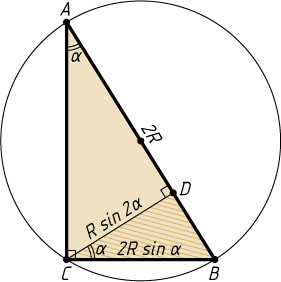
Решение. Пусть AB
— гипотенуза прямоугольного треугольника ABC
. Тогда AB=2R
. Если \angle CAB=\alpha
, то
BC=AB\sin\alpha=2R\sin\alpha.
Если CD
— высота треугольника ABC
, то
CD=BC\cos\angle DCB=BC\cos\alpha=2R\sin\alpha\cos\alpha=R\sin2\alpha.
Источник: Вступительный экзамен на физический факультет МГУ. — 1988, вариант 1, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 48
