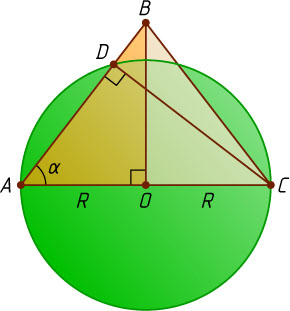
957. В равнобедренном треугольнике ABC
(AB=BC)
проведена высота CD
. Угол BAC
равен \alpha
. Радиус окружности, проходящей через точки A
, C
и D
, равен R
. Найдите площадь треугольника ABC
.
Ответ. R^{2}\tg\alpha
.
Решение. Из точки D
отрезок AC
виден под прямым углом, значит, эта точка лежит на окружности с диаметром AC
, а так как через три точки, не лежащие на одной прямой, проходит единственная окружность, то окружность с диаметром AC
— это окружность, о которой говорится в условии задачи. Пусть O
— её центр. Тогда O
— середина основания AC
равнобедренного треугольника ABC
, поэтому BO
— высота этого треугольника. Из прямоугольного треугольника OAB
находим, что BO=OA\tg\angle OAB=R\tg\alpha
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AC\cdot BO=\frac{1}{2}\cdot2R\cdot R\tg\alpha=R^{2}\tg\alpha.
Источник: Вступительный экзамен на физический факультет МГУ. — 1988, вариант 2, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 49
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.3, с. 86
