958. В треугольник ABC
со стороной BC
, равной 9, вписана окружность, касающаяся стороны BC
в точке D
. Известно, что AD=DC
и косинус угла BCA
равен \frac{2}{3}
. Найдите AC
.
Ответ. 4.
Указание. Примените теорему косинусов.
Решение. Обозначим AC=2x
. Пусть M
— проекция точки D
на AC
. Поскольку треугольник ADC
равнобедренный, то M
— середина AC
.
Из прямоугольного треугольника DMC
находим, что
CD=\frac{MC}{\cos\angle BCA}=\frac{3x}{2},
поэтому BD=BC-CD=9-\frac{3x}{2}
.
Пусть K
и L
— точки касания вписанной в треугольник ABC
окружности со сторонами AC
и AB
соответственно. Тогда
BL=BD=9-\frac{3x}{2},~CK=CD=\frac{3x}{2},
AL=AK=AC-CK=2x-\frac{3x}{2}=\frac{x}{2},
AB=AL+LB=\frac{x}{2}+9-\frac{3x}{2}=9-x.
По теореме косинусов из треугольника ABC
находим, что
AB^{2}=AC^{2}+BC^{2}-2AC\cdot BC\cos\angle BCA,
или
(9-x)^{2}=4x^{2}+81-2\cdot2x\cdot9\cdot\frac{2}{3},
или
3x^{2}-6x=0.
Следовательно, x=2
, AC=2x=4
.
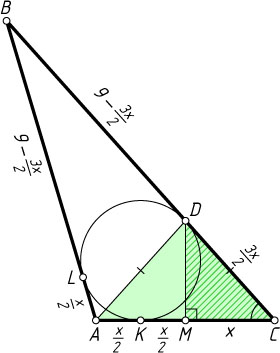
Источник: Вступительный экзамен на химический факультет МГУ. — 1988, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 64
