964. Окружность, проходящая через точку D
и касающаяся сторон AB
и BC
трапеции ABCD
, пересекает стороны AD
и CD
соответственно в точках M
и N
. Известно, что AM:DM=1:3
, CN:DN=4:3
. Найдите основание BC
, если AB=7
и AD=6
.
Ответ. 10
.
Указание. Примените теорему о касательной и секущей.
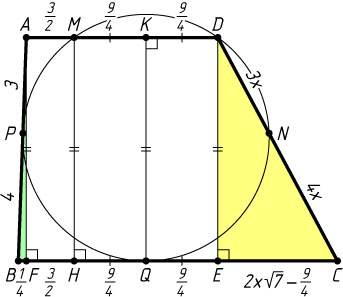
Решение. Пусть P
и Q
— точки касания данной окружности со сторонами соответственно AB
и BC
трапеции ABCD
; K
— середина отрезка DM
; DE
, AF
и MH
— высоты трапеции. Серединный перпендикуляр к отрезку DM
проходит через точку Q
, поэтому KQ
— также высота трапеции. Значит, KQ=DE=MH=AF
.
По теореме о касательной и секущей
AP^{2}=AD\cdot AM=6\cdot\frac{3}{2}=9,~AP=3.
Тогда
BQ=BP=AB-AP=7-3=4,
BF=BQ-FQ=BQ-AK=BQ-(AM+MK)=
=BQ-\left(\frac{1}{4}AD+\frac{1}{2}DM\right)=4-\left(\frac{3}{2}+\frac{9}{4}\right)=\frac{1}{4}.
AF^{2}=AB^{2}-BF^{2}=49-\frac{1}{16}.
Положим CN=4x
, DN=3x
. По теореме о касательной и секущей
QC^{2}=CD\cdot CN=7x\cdot4x=28x^{2},~CQ=2x\sqrt{7}.
Тогда
CE=CQ-QE=CQ-DK=2x\sqrt{7}-\frac{9}{4},
DE^{2}=CD^{2}-CE^{2}=49x^{2}-\left(2x\sqrt{7}-\frac{9}{4}\right)^{2},
а так как DE=AF
, то
49x^{2}-\left(2x\sqrt{7}-\frac{9}{4}\right)^{2}=49-\frac{1}{16}.
После очевидных упрощений получаем квадратное уравнение 7x^{2}+3x\sqrt{7}-18=0
, из которого находим, что x=\frac{3}{\sqrt{7}}
. Следовательно,
BC=BQ+CQ=4+2x\sqrt{7}=4+6=10.