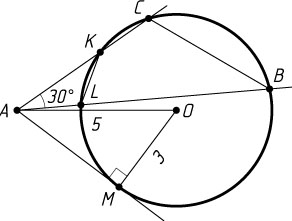
976. Из точки A
, находящейся на расстоянии 5 от центра окружности радиуса 3, проведены две секущие AKC
и ALB
, угол между которыми равен 30^{\circ}
(K
, C
, L
, B
— точки пересечения секущих с окружностью). Найдите площадь треугольника AKL
, если площадь треугольника ABC
равна 10.
Ответ. \frac{8}{5}
.
Указание. Примените теорему о касательной и секущей.
Решение. Проведём из точки A
касательную к данной окружности. Пусть M
— точка касания, O
— центр окружности.
Из прямоугольного треугольника OMA
находим, что
AM^{2}=AO^{2}-OM^{2}=25-9=16.
Тогда
AK\cdot AC=AL\cdot AB=AM^{2}=16.
Поэтому
S_{\triangle AKL}=\frac{1}{2}AK\cdot AL\sin30^{\circ}=\frac{1}{4}AK\cdot AL=
=\frac{1}{4}\cdot\frac{16}{AC}\cdot\frac{16}{AB}=\frac{64}{AC\cdot AB}=\frac{16}{S_{\triangle ABC}}=\frac{16}{10}=\frac{8}{5}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1966, № 4, вариант 1
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 4, № 4, с. 46
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.23, с. 95
