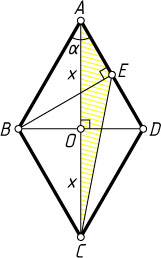
978. В ромбе ABCD
из вершины B
на сторону AD
опущен перпендикуляр BE
. Найдите углы ромба, если 2\sqrt{3}CE=\sqrt{7}AC
.
Ответ. 60^{\circ}
, 120^{\circ}
.
Указание. Примените теорему косинусов к треугольнику CAE
.
Решение. Пусть O
— точка пересечения диагоналей ромба. Положим AC=2x
, \angle BAD=\alpha
. Тогда
AB=\frac{AO}{\cos\angle BAO}=\frac{x}{\cos\frac{\alpha}{2}},~AE=AB\cos\angle BAE=\frac{x\cos\alpha}{\cos\frac{\alpha}{2}},~CE=\frac{AC\sqrt{7}}{2\sqrt{3}}=x\sqrt{\frac{7}{3}}.
По теореме косинусов из треугольника CAE
находим, что
CE^{2}=AE^{2}+AC^{2}-2AE\cdot AC\cos\angle CAE,
или
\frac{7x^{2}}{3}=\frac{x^{2}\cos^{2}\alpha}{\cos^{2}\frac{\alpha}{2}}+4x^{2}-4x^{2}\cos\alpha\frac{\cos\frac{\alpha}{2}}{\cos\frac{\alpha}{2}},~\frac{7}{3}=4+\frac{\cos^{2}\alpha}{\cos^{2}\frac{\alpha}{2}}-4\cos\alpha.
Применив формулу \cos^{2}\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}
, после упрощения получим уравнение
6\cos^{2}\alpha+7\cos\alpha-5=0,
из которого находим, что \cos\alpha=\frac{1}{2}
. Следовательно, \alpha=60^{\circ}
.
Источник: Вступительный экзамен в МФТИ. — 1992, билет 2, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 92-2-2, с. 319
