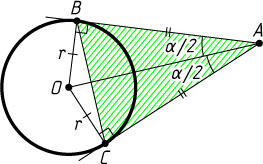
984. Из точки A
, находящейся вне окружности радиуса r
, проведены касательные к окружности — AB
и AC
(B
и C
— точки касания), причём \angle BAC=\alpha
. Найдите площадь треугольника ABC
.
Ответ. \frac{r^{2}}{2}\ctg^{2}\frac{\alpha}{2}\sin\alpha
.
Указание. Найдите AC
из прямоугольного треугольника AOC
(O
— центр окружности).
Решение. Пусть O
— центр окружности. Тогда из прямоугольного треугольника ACO
находим, что
AC=OA\ctg\angle OAC=r\ctg\frac{\alpha}{2}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\angle BAC=\frac{1}{2}AC^{2}\sin\alpha=\frac{r^{2}}{2}\ctg^{2}\frac{\alpha}{2}\sin\alpha.
