987. В треугольнике ABC
угол C
равен 60^{\circ}
, а радиус окружности, описанной вокруг этого треугольника, равен 2\sqrt{3}
. На стороне AB
взята точка D
так, что AD=2DB
и при этом CD=2\sqrt{2}
. Найдите площадь треугольника ABC
.
Ответ. 3\sqrt{2}
.
Указание. С помощью теоремы об отрезках пересекающихся хорд найдите OD
(O
— центр окружности). Треугольник ODC
— прямоугольный.
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
, R=2\sqrt{3}
— её радиус. Тогда
AB=2R\sin\angle C=4\sqrt{3}\cdot\frac{\sqrt{3}}{2}=6.
Поэтому AD=4
, BD=2
.
Поскольку (R-OD)(R+OD)=AD\cdot DB
, то
OD^{2}=R^{2}-AD\cdot DB=12-8=4.
Поэтому OD=2
.
Поскольку OD^{2}+DC^{2}=OC^{2}
, то треугольник ODC
— прямоугольный (\angle ODC=90^{\circ})
. Поскольку треугольник ODB
— равнобедренный, то
\angle DOB=\angle OBD=30^{\circ}.
Поэтому \angle CDB=30^{\circ}
.
Пусть CM
— высота треугольника ABC
. Тогда CM=\frac{1}{2}CD=\sqrt{2}
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot CM=\frac{6\sqrt{2}}{2}=3\sqrt{2}.
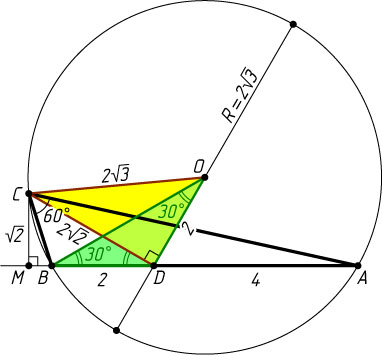
Источник: Вступительный экзамен на химический факультет МГУ. — 1970, № 4, вариант 4
