989. Даны два одинаковых пересекающихся круга. Отношение расстояния между их центрами к радиусу равно 2m
. Третий круг касается внешним образом первых двух и их общей касательной. Найдите отношение площади общей части первых двух кругов к площади третьего круга.
Ответ. \frac{32(\arccos m-m\sqrt{1-m^{2}})}{\pi m^{4}}
.
Указание. Угол между радиусами одного из кругов, проведёнными в точки пересечения окружностей, равен 2\arccos m
. Отрезок общей внешней касательной к двум касающимся кругам, заключённый между точками касания, равен 2\sqrt{Rr}
, где R
и r
— радиусы кругов.
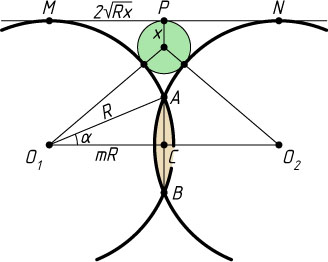
Решение. Пусть O_{1}
, O_{2}
— центры кругов, R
— радиус, A
и B
— точки пересечения, C
— точка пересечения отрезков O_{1}O_{2}
и AB
. Тогда C
— середина AB
и O_{1}O_{2}
, и AB\perp O_{1}O_{2}
.
По условию задачи O_{1}O_{2}=2mR
. Тогда
O_{1}C=mR,~\cos\angle AO_{1}C=\cos\alpha=\frac{O_{1}C}{O_{1}A}=\frac{mR}{R}=m.
Поэтому
\alpha=\arccos m,~S_{\triangle AO_{1}B}=S_{\triangle AO_{2}B}=\frac{1}{2}O_{1}A\cdot O_{1}B\sin2\alpha=
=\frac{1}{2}R^{2}\cdot2\sin\alpha\cos\alpha=R^{2}m\sqrt{1-m^{2}}.
Вычитая из площади сектора AO_{1}B
площадь треугольника AO_{1}B
, получим, что
\frac{1}{2}\cdot2\alpha R^{2}-R^{2}m\sqrt{1-m^{2}}=R^{2}(\arccos m-m\sqrt{1-m^{2}}).
Следовательно, площадь общей части кругов равна
2R^{2}(\arccos m-m\sqrt{1-m^{2}}).
Пусть теперь x
— радиус третьего круга, P
— его точка касания с общей касательной MN
к первым двум кругам (M
и N
— точки касания с первым и вторым кругом). Тогда MN=O_{1}O_{2}
и MP=PN=2\sqrt{Rx}
(см. задачу 365). Поскольку MN=2MP
, то 2\cdot2\sqrt{Rx}=2Rm
. Отсюда находим, что x=\frac{m^{2}R}{4}
, а площадь третьего круга равна \pi x^{2}=\pi m^{4}\cdot\frac{R^{2}}{16}
. Следовательно, искомое отношение равно
\frac{32(\arccos m-m\sqrt{1-m^{2}})}{\pi m^{4}}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1970, № 3, вариант 2
