990. Прямая делит длину окружности в отношении 1:3
. В каком отношении делит она площадь круга?
Ответ. \frac{\pi-2}{3\pi+2}
.
Указание. Длина дуги (и площадь сектора) пропорциональна соответствующему центральному углу.
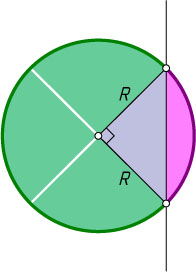
Решение. Поскольку длина дуги окружности пропорциональна соответствующему центральному углу, то меньший из полученных центральных углов составляет \frac{2\pi}{4}=\frac{\pi}{2}
.
Если R
— радиус окружности, то площадь соответствующего сектора равна \frac{\pi R^{2}}{4}
. Вычитая из площади этого сектора площадь соответствующего треугольника, получим, что
\frac{\pi R^{2}}{4}-\frac{R^{2}}{2}=\frac{R^{2}(\pi-2)}{4}.
Оставшаяся часть круга имеет площадь, равную
\pi R^{2}-\frac{R^{2}(\pi-2)}{4}=\frac{R^{2}(3\pi+2)}{4}.
Следовательно, искомое отношение равно \frac{\pi-2}{3\pi+2}
.
Источник: Вступительный экзамен на географический факультет МГУ. — 1970, № 3, вариант 3
