991. Даны две концентрические окружности. Касательная к меньшей окружности делит длину большей окружности в отношении 1:5
. Найдите отношение площадей кругов, ограниченных этими окружностями.
Ответ. \frac{3}{4}
.
Указание. Длина дуги окружности пропорциональна величине соответствующего центрального угла.
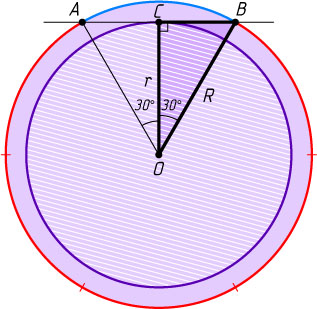
Решение. Пусть A
и B
— точки пересечения данной касательной с большей окружностью, C
— точка касания с меньшей окружностью, O
— центр окружностей, r
и R
— их радиусы (r\lt R)
.
Поскольку длина дуги пропорциональна соответствующему центральному углу, то
\angle AOB=\frac{1}{6}\cdot2\pi=\frac{\pi}{3}.
Из прямоугольного треугольника OCB
находим, что
\frac{r}{R}=\frac{CO}{OB}=\cos\angle COB=\cos\frac{1}{2}\angle AOB=\cos30^{\circ}=\frac{\sqrt{3}}{2}.
Следовательно, отношение площадей данных кругов равно
\frac{\pi r^{2}}{\pi R^{2}}=\left(\frac{r}{R}\right)^{2}=\frac{3}{4}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1970, № 3, вариант 1
