992. Дан ромб с острым углом \alpha
. Какую часть площади ромба составляет площадь вписанного в него круга?
Ответ. \frac{1}{4}\pi\sin\alpha
.
Указание. Высота ромба равна диаметру вписанного в ромб круга.
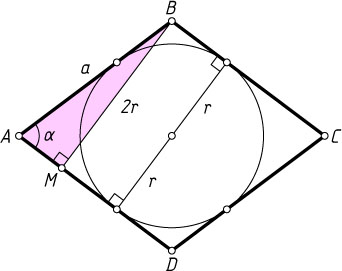
Решение. Пусть сторона ромба ABCD
равна a
и \angle BAD=\alpha
. Тогда площадь ромба равна a^{2}\sin\alpha
.
Из вершины тупого угла B
опустим перпендикуляр BM
на сторону AD
. Тогда
BM=AB\sin\alpha=a\sin\alpha.
Если r
— радиус окружности вписанной в ромб, то
2r=BM=a\sin\alpha.
Поэтому
r=\frac{1}{2}a\sin\alpha
и площадь вписанного в ромб круга равна
\pi r^{2}=\frac{\pi}{4}\cdot a^{2}\sin^{2}\alpha.
Следовательно, искомое отношение равно
\frac{\frac{\pi}{4}a^{2}\sin^{2}\alpha}{a^{2}\sin\alpha}=\frac{1}{4}\pi\sin\alpha.
Источник: Вступительный экзамен на географический факультет МГУ. — 1970, № 3, вариант 2
