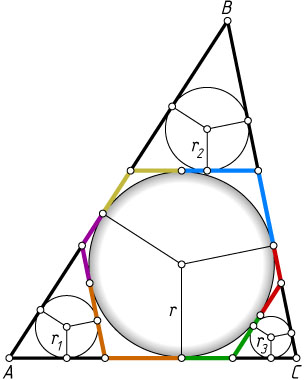
996. В треугольник вписана окружность радиуса r
. Касательные к этой окружности, параллельные сторонам треугольника, отсекают от него три маленьких треугольника. Пусть r_{1}
, r_{2}
, r_{3}
— радиусы вписанных в эти треугольники окружностей. Докажите, что r_{1}+r_{2}+r_{3}=r
.
Указание. Докажите, что сумма периметров маленьких треугольников равна периметру данного треугольника.
Решение. Периметр треугольника, отсекаемого прямой, параллельной стороне BC
, равен сумме расстояний от точки A
до точек касания вписанной в треугольник ABC
окружности со сторонами AB
и AC
. Поэтому сумма периметров маленьких треугольников равна периметру треугольника ABC
, т. е. P_{1}+P_{2}+P_{3}=P
. Из подобия треугольников следует, что
\frac{r_{1}}{r}=\frac{P_{1}}{P},~\frac{r_{2}}{r}=\frac{P_{2}}{P},~\frac{r_{3}}{r}=\frac{P_{3}}{P}.
Складывая почленно эти три равенства, получим, что
\frac{r_{1}+r_{2}+r_{3}}{r}=\frac{P_{1}+P_{2}+P_{3}}{P}=1.
Следовательно, r_{1}+r_{2}+r_{3}=r
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.60, с. 16
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.61, с. 18
Источник: Всесибирская физико-математическая олимпиада. — 2009-2010, второй этап, задача 3, 10 класс
