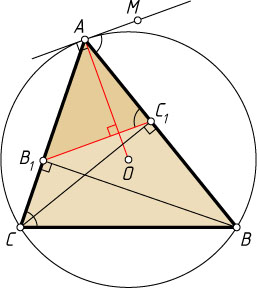
998. В треугольнике ABC
проведены высоты BB_{1}
и CC_{1}
.
а) Докажите, что касательная в точке A
к описанной окружности параллельна прямой B_{1}C_{1}
.
б) Докажите, что B_{1}C_{1}\perp OA
, где O
— центр описанной окружности.
Указание. \angle ACB=\angle AC_{1}B_{1}
.
Решение. На данной касательной возьмём точку M
так, чтобы точки M
и C
лежали по разные стороны от прямой AB
. Тогда
\angle MAB=\angle ACB=\angle B_{1}C_{1}A.
Следовательно, B_{1}C_{1}\parallel MA
. Поскольку AO\perp AM
, то AO\perp B_{1}C_{1}
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.55, с. 17
