999. Биссектриса внешнего угла при вершине C
треугольника ABC
пересекает описанную окружность в точке D
. Докажите, что AD=BD
.
Указание. Выразите углы треугольника ADB
через угол ACB
.
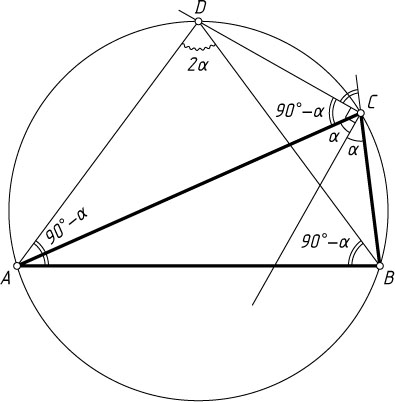
Решение. Пусть точка D
лежит на дуге AC
, не содержащей точки B
. Обозначим \angle ACB=2\alpha
. Тогда
\angle ACD=\frac{1}{2}(180^{\circ}-2\alpha)=90^{\circ}-\alpha.
Поэтому
\angle ABD=\angle ACD=90^{\circ}-\alpha.
Поскольку \angle ADB=\angle ACB=2\alpha
, то
\angle BAD=180^{\circ}-\angle ADB-\angle ABD=180^{\circ}-2\alpha-(90^{\circ}-\alpha)=90^{\circ}-\alpha,
т. е. треугольник ADB
— равнобедренный. Следовательно, AD=BD
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5, с. 31
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5, с. 31
