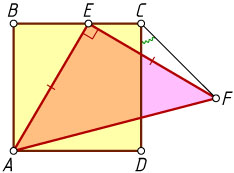
10049. Квадрат ABCD
и равнобедренный прямоугольный треугольник AEF
(\angle AEF=90^{\circ})
расположены так, что точка E
лежит на отрезке BC
(см. рисунок). Найдите угол DCF
.
Ответ. 45^{\circ}
.
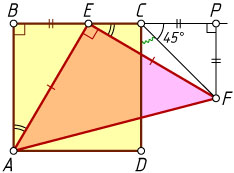
Решение. Первый способ. Пусть P
— основание перпендикуляра, опущенного из точки F
на прямую BC
(рис. 1). Поскольку
\angle FEP=90^{\circ}-\angle BEA=\angle EAB,
прямоугольные треугольники FEP
и EAB
равны (по гипотенузе и острому углу). Следовательно, PF=BE
. Кроме того,
BE=BC-CE=AB-CE=EP-CE=PC.
Таким образом, PF=PC
, т. е. треугольник CPF
прямоугольный и равнобедренный. Значит, \angle FCP=45^{\circ}
, тогда и \angle DCF=45^{\circ}
.
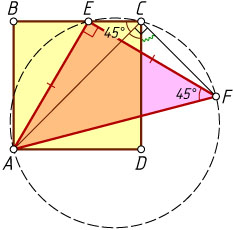
Второй способ. Проведём диагональ AC
. Поскольку \angle ECA=\angle EFA=45^{\circ}
, четырёхугольник ECFA
вписанный (рис. 2). Тогда \angle ACF=\angle AEF=90^{\circ}
Следовательно,
\angle DCF=\angle ACF-\angle ACD=90^{\circ}-45^{\circ}=45^{\circ}.
Источник: Всероссийская олимпиада школьников. — 2015-2016, XLII, окружной этап, 9 класс


