10106. В выпуклом четырёхугольнике две противоположные стороны равны и перпендикулярны, а две другие равны a
и b
. Найдите его площадь.
Ответ. \frac{1}{4}|b^{2}-a^{2}|
.
Решение. Пусть b\gt a
.
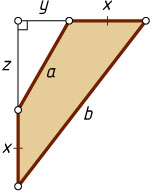
Первый способ. Обозначим длину двух равных сторон через x
. Продолжим их до пересечения и обозначим длины двух получившихся коротких отрезков через y
и z
(рис. 1).
Площадь S
исходного четырёхугольника есть разность площадей двух прямоугольных треугольников: с катетами x+y
и x+z
и с катетами y
и z
. Поэтому
2S=(x+y)(x+z)-yz=x^{2}+xy+xz.
По теореме Пифагора
y^{2}+z^{2}=a^{2},~(x+y)^{2}+(x+z)^{2}=b^{2},
поэтому
b^{2}-a^{2}=2x^{2}+2xy+2xz=4S.
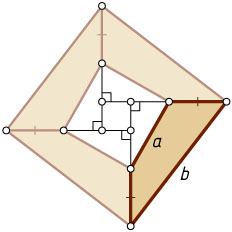
Второй способ. Из четырёх таких четырёхугольников можно сложить квадрат со стороной b
, из которого вырезан квадрат со стороной a
(рис. 2). Поэтому площадь одного четырёхугольника равна \frac{1}{4}(b^{2}-a^{2})
.
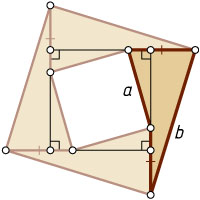
Примечание. Утверждение остаётся верным, даже если отказаться от условия выпуклости.
Автор: Бакаев Е. В.
Источник: Турнир им. М. В. Ломоносова. — 2016


