10107. Шесть равносторонних треугольников расположены, как на рисунке. Докажите, что сумма площадей заштрихованных треугольников равна сумме площадей закрашенных треугольников.
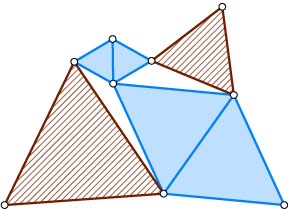
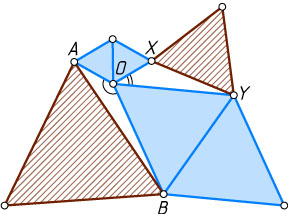
Решение. Обозначим вершины так, как показано на рисунке. Заметим, что
OA=OX,~OB=OY,~\angle AOB+\angle XOY=360^{\circ}-60^{\circ}-120^{\circ}=180^{\circ},
откуда \cos\angle XOY=-\cos\angle AOB
.
Поскольку площадь равностороннего треугольника со стороной t
равна \frac{t^{2}\sqrt{3}}{4}
, достаточно доказать, что
AB^{2}+XY^{2}=2(AO^{2}+BO^{2}).
По теореме косинусов для треугольников ABO
и XYO
получаем, что
AB^{2}=OA^{2}+OB^{2}-2OA\cdot OB\cos\angle AOB,
XY^{2}=OX^{2}+OY^{2}-2OX\cdot OY\cos\angle XOY.
Складывая эти два равенства, получаем требуемое.
Автор: Бакаев Е. В.
Источник: Турнир им. М. В. Ломоносова. — 2015

