10117. На боковой стороне BC
равнобедренного треугольника ABC
с основанием AC
взяты точки M
и N
так, что AN=MN
и \angle BAM=\angle NAC
(см. рисунок). Докажите, что \angle MAC=60^{\circ}
.
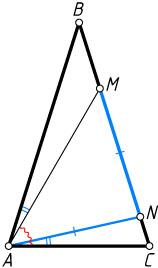
Решение. Рассмотрим случай, когда точка M
лежит между B
и N
. Обозначим
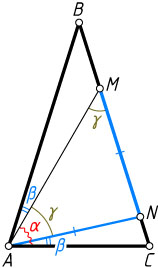
\angle MAC=\alpha,~\angle BAM=\angle NAC=\beta,~\angle MAN=\angle AMN=\gamma.
По теореме о внешнем угле треугольника
\gamma=\angle AMN=\angle B+\angle BAM=180^{\circ}-2\angle BAC+\beta=
=180^{\circ}-2(\alpha+\beta)+\beta=180^{\circ}-2\alpha-\beta.
Следовательно,
\angle MAC=\alpha=\angle MAN+\angle NAC=\gamma+\beta=
=(180^{\circ}-2\alpha-\beta)+\beta=180^{\circ}-2\alpha,
откуда \alpha=60^{\circ}
.
Источник: Произволов В. В. Задачи на вырост. — М.: МИРОС, 1995. — № 13, с. 38

