10155. Окружность с центром O
, вписанная в треугольник ABC
, касается его сторон BC
, AB
и AC
в точках K
, L
и M
соответственно. Прямая KM
вторично пересекает в точке P
окружность радиуса AM
с центром A
.
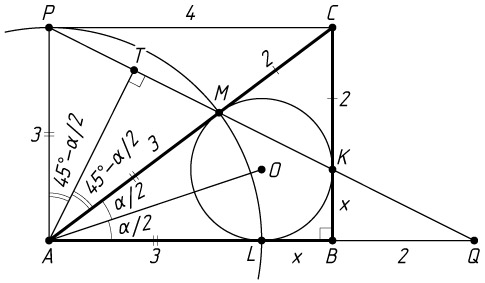
а) Докажите, что AP\parallel BC
.
б) Пусть Q
— точка пересечения прямых KM
и AB
, а T
— такая точка на отрезке PQ
, что \angle OAT=45^{\circ}
Найдите QT
, если \angle ABC=90^{\circ}
, AM=3
, CM=2
.
Ответ. \frac{12}{\sqrt{5}}
.
Решение. а) Поскольку CK=CM
и AP=AM
, треугольники MCK
и PAM
равнобедренные, причём \angle CMK=\angle AMP
— углы при их основаниях MK
и MP
. Значит, \angle MKC=\angle MPA
. Следовательно, AP\parallel BC
.
б) Обозначим BK=BL=x
. Тогда
CK=CM=2,~AL=AM=3,~BC=2+x,~AB=3+x.
По теореме Пифагора
AC^{2}=BC^{2}+AB^{2},~\mbox{или}~25=(2+x)^{2}+(3+x)^{2},
откуда x=1
. Значит, BC=3
, AB=4
.
Поскольку BC=AP=3
и BC\parallel AP
, четырёхугольник ABCP
— прямоугольник, значит, CP=AB=4
.
Треугольник AMQ
подобен треугольнику CMP
с коэффициентом \frac{AM}{MC}=\frac{3}{2}
, поэтому
AQ=\frac{3}{2}CP=\frac{3}{2}\cdot4=6.
Обозначим \angle BAC=\alpha
. Тогда
\angle MAO=\frac{\alpha}{2},~\angle MAT=45^{\circ}-\frac{\alpha}{2},
\angle PAT=90^{\circ}-\angle QAT=90^{\circ}-\left(45^{\circ}+\frac{\alpha}{2}\right)=45^{\circ}-\frac{\alpha}{2},
поэтому AT
— биссектриса, а значит, и высота равнобедренного треугольника MAP
.
В прямоугольном треугольнике ATQ
известно, что
AQ=6,~\tg\angle AQT=\tg\angle AQP=\frac{AP}{AQ}=\frac{3}{6}=\frac{1}{2}.
Тогда \cos\angle AQT=\frac{2}{\sqrt{5}}
. Следовательно,
QT=AQ\cos\angle AQT=6\cdot\frac{2}{\sqrt{5}}=\frac{12}{\sqrt{5}}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2017

