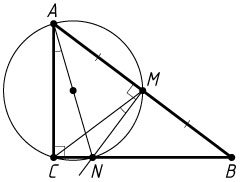
10202. Точка M
— середина гипотенузы AB
прямоугольного треугольника ABC
. Серединный перпендикуляр к гипотенузе пересекает катет BC
в точке N
.
а) Докажите, что \angle CAN=\angle CMN
.
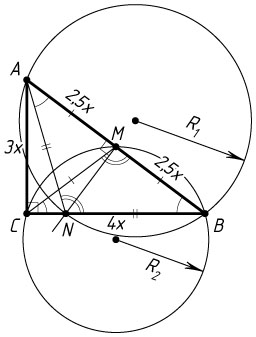
б) Найдите отношение радиусов окружностей, описанных около треугольников ANB
и CBM
, если \tg\angle BAC=\frac{4}{3}
.
Ответ. \frac{5}{4}
.
Решение. а) Из точек C
и M
отрезок AN
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AN
. Вписанные в эту окружность углы CAN
и CMN
опираются на одну и ту же дугу, следовательно, они равны.
б) Вписанные углы MCN
и MAN
также опираются на одну дугу, поэтому
\angle BAN=\angle MAN=\angle MCN=\angle MCB,
а так как CM
— медиана прямоугольного треугольника ABC
, проведённая из вершины прямого угла, то \angle MCB=\angle MBC
. Таким образом,
\angle MBC=\angle BCM=\angle BAN.
Равнобедренные треугольники ANB
и CMB
подобны по двум углам, причём коэффициент подобия равен отношению их оснований, т. е. k=\frac{AB}{BC}=\frac{1}{\sin\angle BAC}
. Поскольку
\frac{1}{\sin\angle BAC}=\sqrt{1+\ctg^{2}\angle BAC}=\sqrt{1+\frac{9}{16}}=\frac{5}{4},
а отношение радиусов описанных окружностей подобных треугольников равно коэффициенту подобия, то
\frac{R_{\triangle ANB}}{R_{\triangle CBM}}=k=\frac{1}{\sin\angle BAC}=\frac{5}{4}.
Источник: ЕГЭ. — 2017, досрочный экзамен (резерв), 14 апреля

