10222. На рисунке изображены окружности с центрами A
и B
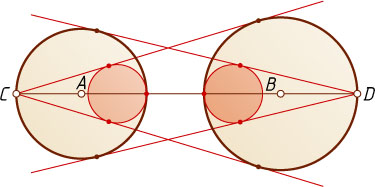
, лежащие одна вне другой. Прямые, проходящие через точку C
, касаются второй окружности, а прямые, проходящие через точку D
, касаются первой. Докажите, что изображённые на рисунке две другие малые окружности имеют равные радиусы.
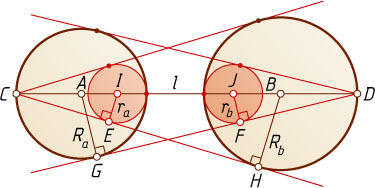
Решение. Пусть R_{a}
и R_{b}
— радиусы данных окружностей с центрами A
и B
соответственно, а I
и J
— центры малых окружностей радиусов r_{a}
и r_{b}
, расположенные внутри окружностей с центрами A
и B
соответственно; одна из прямых, проходящих через точку A
касается окружности с центром B
в точке H
, а ближайшей малой окружности с центром I
— в точке E
; одна из прямых, проходящих через точку B
касается окружности с центром A
в точке G
, а малой окружности с центром J
— в точке F
(точки E
, H
, F
и G
расположены по одну сторону от прямой AB
). Обозначим через l
расстояние между ближайшими точками окружностей с центрами A
и B
.
Прямоугольные треугольники CHB
и CEI
подобны, поэтому
\frac{BH}{IE}=\frac{R_{b}}{r_{a}}=\frac{2R_{a}+l+R_{b}}{2R_{a}-r_{a}},
откуда
r_{a}=\frac{2R_{a}R_{b}}{2R_{a}+2R_{b}+l}.
Прямоугольные треугольники DGA
и DFJ
подобны, поэтому
\frac{AG}{JF}=\frac{R_{a}}{r_{b}}=\frac{2R_{b}+l+R_{a}}{2R_{b}-r_{b}},
откуда
r_{b}=\frac{2R_{a}R_{b}}{2R_{a}+2R_{b}+l}.
Следовательно, r_{a}=r_{b}
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1989, № 2, задача 1311 (1988, с. 44), с. 62

