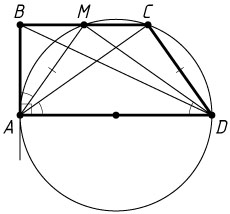
10236. Дана прямоугольная трапеция ABCD
с прямым углом при вершине A
. Окружность, построенная на большем основании AD
как на диаметре, проходит через вершину C
и пересекает меньшее основание BC
в точке M
.
а) Докажите, что \angle BAM=\angle CAD
.
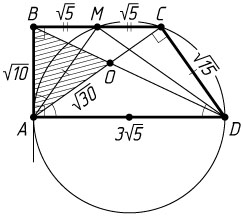
б) Диагонали трапеции пересекаются в точке O
. Найдите площадь треугольника AOB
, если AB=\sqrt{10}
, а M
— середина BC
.
Ответ. 3\sqrt{2}
.
Решение. а) Поскольку AD
— диаметр окружности и AD\perp AB
, то AB
— касательная к окружности. Из теоремы об угле между касательной и хордой следует, что \angle BAM=\angle ADM
. Трапеция AMCD
вписана в окружность, поэтому она равнобедренная, и её диагонали образуют равные углы с основаниями. Значит, \angle ADM=\angle CAD
. Следовательно, \angle BAM=\angle CAD
.
б) По теореме о касательной и секущей AB^{2}=BM\cdot BC
, или 10=2BM^{2}
, откуда BM=\sqrt{5}
. Тогда
BC=2BM=2\sqrt{5},~CD=AM=\sqrt{AB^{2}+BM^{2}}=\sqrt{10+5}=\sqrt{15},
AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{10+20}=\sqrt{30}.
Точка C
лежит на окружности с диаметром AD
, поэтому \angle ACD=90^{\circ}
. По теореме Пифагора
AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{30+15}=\sqrt{45}=3\sqrt{5}.
Значит,
\frac{BC}{AD}=\frac{2\sqrt{5}}{3\sqrt{5}}=\frac{2}{3}.
Следовательно,
S_{\triangle AOB}=\frac{BO}{BD}S_{\triangle ABD}=\frac{2}{5}\cdot\frac{1}{2}AD\cdot AB=\frac{1}{5}\cdot3\sqrt{5}\cdot\sqrt{10}=3\sqrt{2}.
Примечание. Можно и так: найдём высоту OH
треугольника AOB
из подобия треугольников AHO
и ABC
, а затем площадь треугольника AOB
.
Источник: ЕГЭ. — 2017, 2 июня

