10237. Окружности с центрами O_{1}
и O_{2}
пересекаются в точках A
и B
, причём точки O_{1}
и O_{2}
лежат по разные стороны от прямой AB
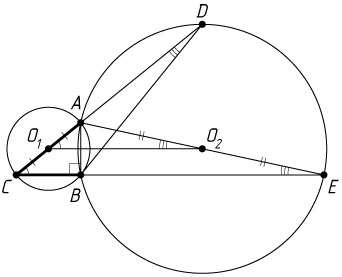
. Продолжения диаметра CA
первой окружности и хорды CB
этой же окружности пересекают вторую окружность в точках D
и E
соответственно.
а) Докажите, что треугольник CBD
подобен треугольнику, вершины которого — центры окружностей и точка A
.
б) Найдите AD
, если \angle DAE=\angle BAC
, радиус второй окружности втрое больше радиуса первой и AB=3
.
Ответ. 9.
Решение. а) Поскольку \angle ABE=90^{\circ}
, отрезок AE
— диаметр окружности с центром O_{2}
. Значит, точка O_{2}
середина стороны AE
треугольника CAE
, а отрезок O_{1}O_{2}
— средняя линия этого треугольника, поэтому
\angle AO_{2}O_{1}=\angle AEC,~\angle AO_{1}O_{2}=\angle ACE=\angle DCB,
а так как вписанные во вторую окружность углы ADB
и AEB
опираются на одну и ту же дугу, то
\angle AO_{2}O_{1}=\angle AEC=\angle AEB=\angle ADB=\angle CDB.
Следовательно, треугольники CBD
и O_{1}AO_{2}
подобны по двум углам.
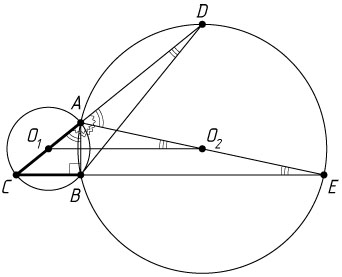
б) Заметим, что
\angle BAD=\angle BAE+\angle DAE=\angle BAE+\angle BAC=\angle EAC,
а так как
\angle BDA=\angle BEA=\angle CEA,
то треугольник ABD
подобен треугольнику ACE
по двум углам. Значит, \frac{AD}{AB}=\frac{AE}{AC}=3
. Следовательно, AD=3AB=9
.
Источник: ЕГЭ. — 2017, 2 июня

