10238. Дана трапеция. Сумма оснований равна 13, диагонали 5 и 12.
а) Докажите, что диагонали перпендикулярны.
б) Найдите высоту трапеции.
Ответ. \frac{60}{13}
.
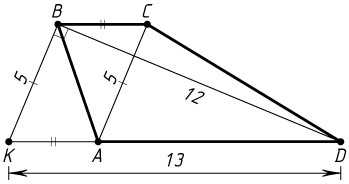
Решение. а) Пусть ABCD
— трапеция с диагоналями AC=5
, BD=12
и суммой оснований AD+BC=13
. Через вершину B
проведём прямую, параллельную AC
. Пусть K
— точка её пересечения с прямой AD
. Тогда ACBK
— параллелограмм, поэтому BK=AC=5
, AK=BC
, а угол между диагоналями трапеции равен углу DBK
. Треугольник DBK
прямоугольный с прямым углом DBK
, так как
DK^{2}=(AK+AD)^{2}=13^{2}=5^{2}+12^{2}=KB^{2}+BD^{2}.
Следовательно, угол между диагоналями трапеции ABCD
равен 90^{\circ}
.
б) Пусть BH
— высота трапеции. Тогда BH
— высота прямоугольного треугольника DBK
, опущенная на гипотенузу. Следовательно,
BH=\frac{BK\cdot BD}{AD}=\frac{5\cdot12}{13}=\frac{60}{13}.

Источник: ЕГЭ. — 2017, 2 июня

