10357. Дан параллелограмм ABCD
. Прямая, параллельная стороне AB
, пересекает биссектрисы углов A
и C
в точках P
и Q
соответственно. Докажите, что углы ADP
и ABQ
равны.
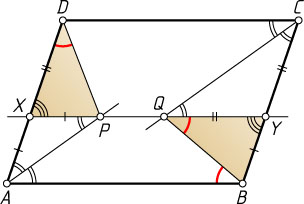
Решение. Первый способ. Рассмотрим случай, изображённый на рис. 1.
Пусть указанная прямая пересекает стороны AD
и BC
в точках X
и Y
соответственно. Луч CQ
— биссектриса угла BCD
, поэтому
\angle YCQ=\angle DCQ=\angle YQC.
Значит, YQ=YC=XD
. Аналогично XP=XA=YB
.
Кроме того, прямые BC
и AD
параллельны, поэтому \angle BYQ=\angle DXP
. Значит, треугольники BYQ
и PXD
равны. Следовательно,
\angle ADP=\angle BQY=\angle ABQ.
Аналогично для других случаев.
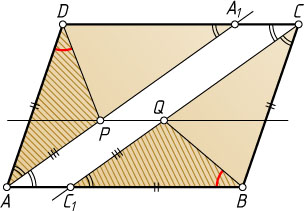
Второй способ. Пусть A_{1}
и C_{1}
— точки пересечения биссектрис углов A
и C
с прямыми CD
и AB
соответственно (рис. 2). Тогда
\angle AA_{1}D=\angle A_{1}AD=\angle CC_{1}B=\angle C_{1}CB.
Кроме того, AD=BC
, поэтому равнобедренные треугольники ADA_{1}
и CBC_{1}
равны.
Заметим, что APQC_{1}
— параллелограмм, поэтому AP=C_{1}Q
. Тогда треугольники APD
и C_{1}QB
равны по двум сторонам (AD=C_{1}B
, AP=C_{1}Q
) и углу между ними. Следовательно, \angle ADP=\angle ABQ
.
Автор: Акопян А. В.
Источник: Московская устная олимпиада по геометрии. — 2005, № 2, 8-9 классы

