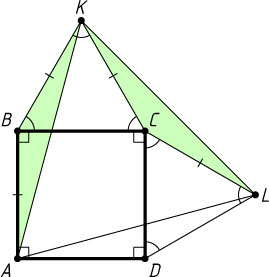
1038. На сторонах BC
и CD
квадрата ABCD
построены внешним образом правильные треугольники BCK
и DCL
. Докажите, что треугольник AKL
— правильный.
Указание. Треугольники ABK
, KCL
, ADL
равны.
Решение. Поскольку
AB=BK=CK=CL,
\angle ABK=\angle ABC+\angle CBK=90^{\circ}+60^{\circ}=150^{\circ},
\angle KCL=360^{\circ}-\angle DCL-\angle DCB-\angle BCK=360^{\circ}-60^{\circ}-90^{\circ}-60^{\circ}=150^{\circ},
то треугольники ABK
и KCL
равны по двум сторонам и углу между ними.
Следовательно, KL=AK
. Аналогично KL=AL
.