10386. Два равносторонних треугольника ABC
и CDE
имеют общую вершину (см.рис). Найдите угол между прямыми AD
и BE
.
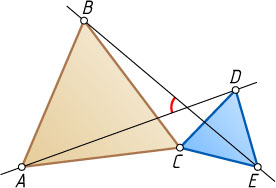
Ответ. 60^\circ
.
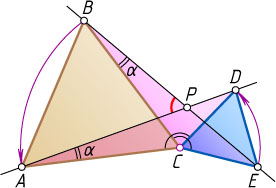
Решение. Первый способ. Пусть P
— точка пересечения AD
и BE
(рис. 1). Обозначим \angle CBE=\alpha
. Заметим, что треугольники ACD
и BCE
равны по двум сторонам и углу между ними), откуда следует, что \angle DAC=\angle CBE=\alpha
. Тогда
\angle APB=180^{\circ}-(\angle PAB+\angle PBA)=180^{\circ}-((\angle CAB)-\alpha)+(\angle CBA+\alpha))=
=180^{\circ}-(\angle CAB+\angle CBA)=180^{\circ}-(60^{\circ}+60^{\circ})=60^{\circ}.
Второй способ. При повороте с центром C
и углом 60^{\circ}
точка B
переходит в A
, точка E
— в D
, значит, образ прямой BE
— прямая AD
. Следовательно, угол между этими прямыми равен 60^\circ
.
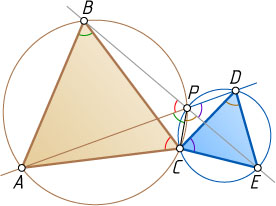
Третий способ. Пусть P
— вторая точка пересечения окружностей, описанных около треугольников ABC
и CDE
(рис. 2). Тогда
\angle APC=\angle ABC=60^{\circ}
(вписанные углы, опирающиеся на одну дугу) и
\angle DPC=180^{\circ}-\angle DEC=120^{\circ}
(вписанные углы, опирающиеся на дополняющие друг друга до окружности дуги). Значит, точки A
, P
и D
лежат на одной прямой. Аналогично для точек B
, P
и E
. Тогда
\angle APB=\angle ACB=60^{\circ}
(вписанные углы, опирающиеся на одну дугу).