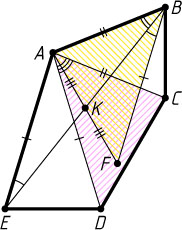
1040. В выпуклом пятиугольнике ABCDE
известно, что AE=AD
, AC=AB
и \angle DAC=\angle AEB+\angle ABE
. Докажите, что сторона DC
в два раза больше медианы AK
треугольника ABE
.
Указание. Отложите на продолжении медианы AK
за точку K
отрезок KF
, равный AK
, и докажите равенство треугольников ABF
и CAD
.
Решение. Отложим на продолжении медианы AK
за точку K
отрезок KF
, равный AK
. Из равенства треугольников BKF
и EKA
следует, что BF=AE=AD
и \angle KBF=\angle KEA
, поэтому
\angle ABF=\angle ABK+\angle KBF=\angle DAC.
Кроме того, AB=AC
, поэтому треугольники ABF
и CAD
равны. Следовательно, CD=AF=2AK
.
Источник: Турнир городов. — 1983-1984, V, весенний тур, младшие классы, тренировочный вариант
Источник: Журнал «Квант». — 1984, № 9, с. 54, задача 6
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1983-1984, L, 7 класс
