1041. Внутри квадрата ABCD
взята точка P
так, что \angle PBA=\angle PAB=15^{\circ}
. Докажите, что CPD
— равносторонний треугольник.
Указание. Постройте на стороне AD
квадрата внутренним образом треугольник AQD
, равный треугольнику APB
.
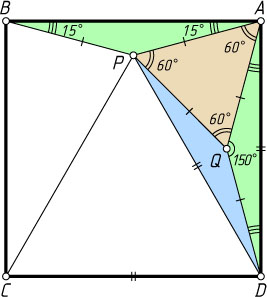
Решение. Первый способ. Построим на стороне AD
квадрата внутренним образом треугольник AQD
, равный треугольнику APB
(рис. 1). Тогда
\angle PAQ=90^{\circ}-15^{\circ}-15^{\circ}=60^{\circ}~\mbox{и}~AP=AQ.
Поэтому треугольник APQ
— равносторонний.
Поскольку
\angle PQD=360^{\circ}-60^{\circ}-150^{\circ}=150^{\circ},
то треугольники PQD
и AQD
равны (по двум сторонам и углу между ними). Следовательно, PD=DA=CD
. Аналогично CP=CD
.
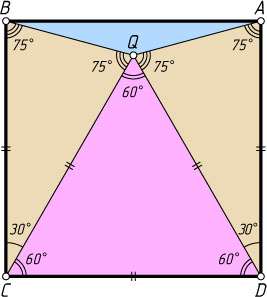
Второй способ. Возьмём внутри квадрата ABCD
такую точку Q
, что треугольник CQD
— равносторонний (рис. 2). Поскольку CQ=CD=BC
, то треугольник BCQ
— равнобедренный, поэтому
\angle CBQ=\frac{1}{2}(180^{\circ}-\angle BCQ)=\frac{1}{2}(180^{\circ}-30^{\circ})=75^{\circ}.
Тогда
\angle QBA=90^{\circ}-\angle CBQ=90^{\circ}-75^{\circ}=15^{\circ}.
Аналогично докажем, что \angle QAB=15^{\circ}
.
Поскольку в заданной полуплоскости от данного луча можно отложить ровно один угол с заданной градусной мерой, то точка Q
совпадает с точкой P
. Следовательно, треугольник CPD
, о котором говорится в условии задачи, совпадает с равносторонним треугольником CQD
.
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 2, с. 38
Источник: Яковлев Г. Н. и др. Всероссийские математические олимпиады школьников. — М.: Просвещение, 1992. — № 34, с. 10
Источник: Всероссийская олимпиада школьников. — 1977-78, IV, III этап, 9 класс

