10477. Точки A_{1}
, B_{1}
, C_{1}
— середины сторон соответственно BC
, AC
, AB
треугольника ABC
. Углы треугольника при вершинах A
и C
равны 120^{\circ}
и 15^{\circ}
соответственно, AH
— высота треугольника.
а) Докажите, что \angle A_{1}C_{1}B_{1}=\angle A_{1}HB_{1}
.
б) Найдите A_{1}H
, если BC=8\sqrt{3}
.
Ответ. 4.
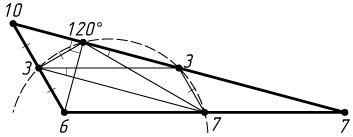
Решение. а) По теореме о средней линии треугольника B_{1}C_{1}\parallel BC
и A_{1}B_{1}=\frac{1}{2}AB
. Кроме того, отрезок HC_{1}
— медиана прямоугольного треугольника AHB
, проведённая из вершины прямого угла, поэтому HC_{1}=\frac{1}{2}AB=A_{1}B_{1}
. Значит, A_{1}HB_{1}C_{1}
— равнобедренная трапеция с основаниями A_{1}H
и B_{1}C_{1}
. Около неё можно описать окружность. Вписанные в эту окружность углы A_{1}C_{1}B_{1}
и A_{1}HB_{1}
опираются на одну и ту же дугу, следовательно, они равны.
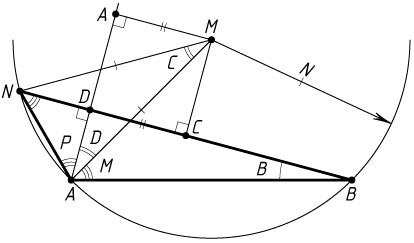
б) Пусть O
— центр окружности радиуса R
, описанной около треугольника ABC
. Поскольку \angle BAC\gt90^{\circ}
, точки A
и O
лежат по разные стороны от прямой BC
. По теореме синусов
R=\frac{BC}{2\sin120^{\circ}}=\frac{8\sqrt{3}}{2\cdot\frac{\sqrt{3}}{2}}=8.
Центральный угол AOB
вдвое больше вписанного угла ACB
, т. е. \angle AOB=30^{\circ}
. Тогда углы OBA
и OAB
при основании равнобедренного треугольника AOB
равны по 75^{\circ}
, а так как \angle BAH=\angle ABH=45^{\circ}
, то
\angle OAH=\angle OAB-\angle HAB=75^{\circ}-45^{\circ}=30^{\circ}.
Пусть OF
— перпендикуляр, опущенный из центра окружности на прямую AH
. Катет прямоугольного треугольника AFO
, лежащий против угла 30^{\circ}
, равен половине гипотенузы, следовательно,
A_{1}H=OF=\frac{1}{2}OA=\frac{1}{2}R=4.
Источник: ЕГЭ. — 2017, досрочный экзамен, 31 марта

