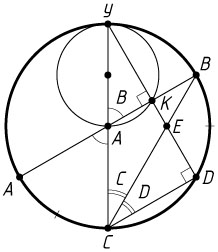
10478. Две окружности касаются внутренним образом в точке A
, причём меньшая окружность проходит через центр O
большей. Диаметр BC
большей окружности вторично пересекает меньшую окружность в точке M
, отличной от A
. Лучи AO
и AM
пересекают большую окружность в точках P
и Q
.
а) Докажите, что PQ\parallel BC
.
б) Известно, что угол AOC
равен 60^{\circ}
. В каком отношении прямая PC
делит отрезок AQ
?
Ответ. 1:2
.
Решение. а) Линия центров касающихся окружностей проходит через точку их касания, поэтому точка O
лежит на диаметре AP
большей окружности, а OA
— диаметр меньшей окружности.
Пусть точки P
и Q
лежат на прямых AO
и AM
соответственно. Точка M
лежит на окружности с диаметром OA
, поэтому \angle AMO=90^{\circ}
. Значит, OM\perp AQ
. Точка Q
лежит на окружности с диаметром AP
, значит, PQ\perp AQ
. Прямые OM
и PQ
перпендикулярны одной и той же прямой AQ
, значит, PQ\parallel OM
. Следовательно, PQ\parallel BC
.
б) Дуги окружности, заключённые между параллельными хордами, равны, поэтому
\angle CPQ=\frac{1}{2}\smile CQ=\frac{1}{2}\smile BP=\frac{1}{2}\angle BOP=\frac{1}{2}\angle AOC=30^{\circ}
(\smile CQ
и \smile BP
— градусные меры дуг CQ
и BP
, не содержащих точек B
и C
соответственно), а так как \angle APQ=\angle AOC=60^{\circ}
, то луч PC
— биссектриса угла APQ
.
Пусть K
— точка пересечения AQ
и PC
. Тогда PK
— биссектриса прямоугольного треугольника APQ
. Следовательно,
\frac{QK}{AK}=\frac{PQ}{AP}=\cos\angle APQ=\cos\angle AOC=\cos60^{\circ}=\frac{1}{2}.
Источник: ЕГЭ. — 2017, 2 июня

