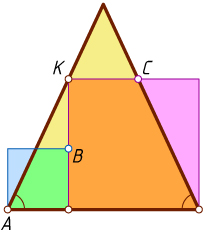
10482. Два квадрата и равнобедренный треугольник расположены так, как показано на рисунке (вершина K
большого квадрата лежит на стороне треугольника). Докажите, что точки A
, B
и C
лежат на одной прямой.
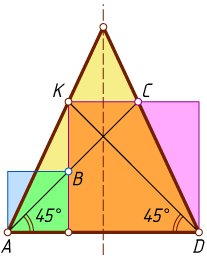
Решение. Первый способ. У равнобедренного треугольника есть ось симметрии. При симметрии относительно этой оси точка K
переходит в C
, а точка D
переходит в A
(рис. 1). Значит, AC
образует тот же угол с основанием, что и диагональ KD
квадрата, т. е. 45^{\circ}
. Но AB
тоже образует с основанием угол 45^{\circ}
как диагональ меньшего квадрата. Значит, точки A
, B
и C
действительно лежат на одной прямой.
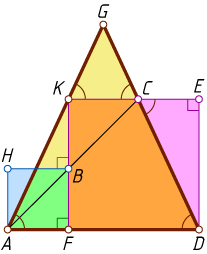
Второй способ (без использования симметрии). Введём обозначения так, как показано на рис. 2, и проведём отрезки AB
и BC
. Поскольку \angle ABH=45^{\circ}
, достаточно доказать, что
\angle KBC=\angle BCK=45^{\circ}
(тогда
\angle ABH+\angle HBK+\angle KBC=45^{\circ}+90^{\circ}+45^{\circ}=180^{\circ},
что равносильно утверждению задачи).
Используя равенство соответственных углов при параллельных прямых и равнобедренность треугольника AGD
, получим, что
\angle GKC=\angle GAD=\angle GDA=\angle GCK.
Значит, GK=GC
, поэтому AK=CD
. Тогда равны прямоугольные треугольники AKF
и CDE
(по гипотенузе и катету). Следовательно, CE=AF=BF
, поэтому BK=CK
, откуда
\angle KBC=\angle BCK=45^{\circ}.
Что и требовалось доказать.
Автор: Евдокимов М. А.
Источник: Московская математическая олимпиада. — 2018, LXXXI, 7 класс
Источник: Журнал «Квант». — 2018, № 3, с. 29, задача 3


