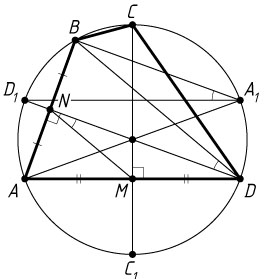
10493. Четырёхугольник ABCD
вписан в окружность. Диаметр CC_{1}
перпендикулярен стороне AD
и пересекает её в точке M
, а диаметр DD_{1}
перпендикулярен стороне AB
и пересекает её в точке N
.
а) Пусть AA_{1}
— также диаметр окружности. Докажите, что \angle DNM=\angle BA_{1}D_{1}
.
б) Найдите углы четырёхугольника ABCD
, если угол CDB
вдвое меньше угла ADB
.
Ответ. 72^{\circ}
, 126^{\circ}
, 108^{\circ}
, 54^{\circ}
.
Решение. а) Диаметр, перпендикулярный хорде, делит её пополам. Значит, M
и N
— середины сторон AD
и AB
соответственно. Отрезок MN
— средняя линия треугольника BAD
, поэтому MN\parallel BD
. Тогда
\angle BDD_{1}=\angle BDN=\angle DNM.
Вписанные углы BA_{1}D_{1}
и BDD_{1}
опираются на одну и ту же дугу, поэтому \angle BA_{1}D_{1}=\angle BDD_{1}
. Следовательно, \angle DNM=\angle BA_{1}D_{1}
.
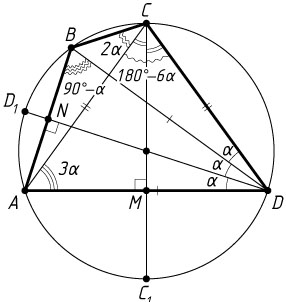
б) Треугольники ADB
и ACD
равнобедренные, поэтому их высоты DN
и CM
являются биссектрисами. Обозначим \angle ADD_{1}=\angle BDD_{1}=\alpha
. Тогда
\angle CDB=\frac{1}{2}\angle ADB=\angle ADD_{1}=\alpha,
\angle CAD=\angle ADC=3\alpha,~\angle ACD=180^{\circ}-6\alpha,~\angle ACB=\angle ADB=2\alpha,
\angle BCD=\angle ACB+\angle ACD=2\alpha+180^{\circ}-6\alpha=180^{\circ}-4\alpha,
\angle BAD=\angle ABD=90^{\circ}-\angle BDD_{1}=90^{\circ}-\alpha,
Сумма противоположных углов вписанного четырёхугольника равна 180^{\circ}
, поэтому \angle BAD+\angle BCD=180^{\circ}
, или
(90^{\circ}-\alpha)+(180^{\circ}-4\alpha)=180^{\circ}~\Leftrightarrow~5\alpha=90^{\circ}~\Leftrightarrow~\alpha=18^{\circ}.
Следовательно,
\angle ADB=3\alpha=54^{\circ},~\angle ABD=180^{\circ}-\angle ADB=180^{\circ}-54^{\circ}=126^{\circ},
\angle BAD=90^{\circ}-\alpha=90^{\circ}-18^{\circ}=72^{\circ},~\angle BCD=180^{\circ}-72^{\circ}=108^{\circ}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2018, тренировочная работа, 6 марта

