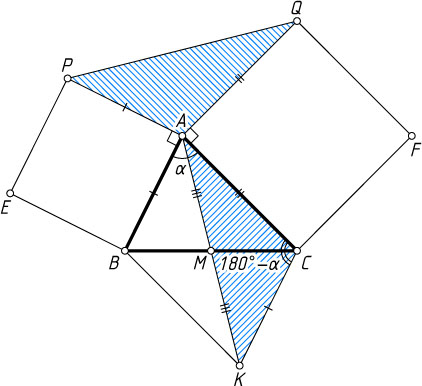
1050. На двух сторонах треугольника вне его построены квадраты. Докажите, что отрезок, соединяющий концы сторон квадратов, выходящих из одной вершины треугольника, в два раза больше медианы треугольника, выходящей из той же вершины.
Указание. Отложите на продолжении указанной медианы AM
за точку M
отрезок, равный медиане, и примените признак равенства треугольников.
Решение. Пусть AP
и AQ
— указанные стороны квадратов APEB
и AQFC
, AM
— медиана треугольника ABC
, \angle BAC=\alpha
.
Отложим на продолжении медианы AM
за точку M
отрезок MK
, равный отрезку AM
. Тогда
CK=AB=AP,AC=AQ,
\angle PAQ=360^{\circ}-90^{\circ}-90^{\circ}-\alpha=180^{\circ}-\alpha=\angle KCA.
Поэтому треугольники ACK
и QAP
равны по двум сторонам и углу между ними. Следовательно, AK=PQ
и AM=\frac{1}{2}AK=\frac{1}{2}PQ
.
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 440, с. 113
