10507. Окружность проходит через вершины A
, B
и D
параллелограмма ABCD
, пересекает сторону BC
в точках B
и M
, и пересекает продолжение стороны CD
за точку D
в точке N
.
а) Докажите, что отрезки AM
и AN
равны.
б) Найдите отношение длин отрезков CD
и DN
, если AB:BC=1:3
, а \cos\angle BAD=0{,}4
.
Ответ. 5:7
.
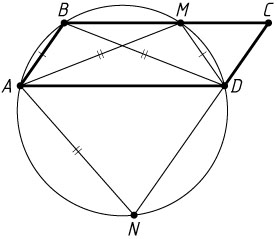
Решение. а) Трапеция ABMD
вписана в окружность, значит, она равнобокая. Диагонали равнобокой трапеции равны, поэтому AM=BD
. Трапеция ABDN
вписана в окружность, значит, она также равнобокая, поэтому BD=AN
. Следовательно, AM=AN
.
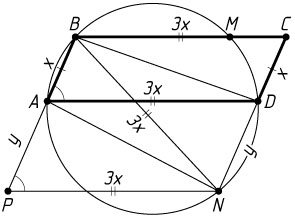
б) Обозначим CD=AB=x
, DN=y
. Тогда AD=BC=3x
. Рассмотрим равнобокую трапецию ABDN
с основаниями AB=x
, DN=y
и диагоналями BN=AD=3x
. Через точку N
проведём прямую, параллельную AD
. Пусть P
— точка пересечения этой прямой с продолжением отрезка AB
. Рассмотрим треугольник BNP
со сторонами BP=x+y
, BN=AD=NP=3x
, и углом, BPN
, равным углу BAD
. По теореме косинусов
BN^{2}=BP^{2}+NP^{2}-2\cdot BP\cdot NP\cos\angle BPN,
или
9x^{2}=(x+y)^{2}+9x^{2}-2(x+y)\cdot3x\cdot\frac{2}{5},~~5y^{2}-2xy-7x^{2}=0,
откуда y=\frac{7}{5}x
. Следовательно,
\frac{CD}{DN}=\frac{x}{y}=\frac{x}{\frac{7}{5}x}=\frac{5}{7}.
Источник: ЕГЭ. — 2018, 1 июня

