10508. Окружность с центром O_{1}
касается оснований BC
и AD
и боковой стороны AB
трапеции ABCD
. Окружность с центром O_{2}
касается сторон BC
, CD
и AD
. Известно, что AB=10
, BC=9
, CD=30
, AD=39
.
а) Докажите, что прямая O_{1}O_{2}
параллельна основаниям трапеции ABCD
.
б) Найдите O_{1}O_{2}
.
Ответ. 4
.
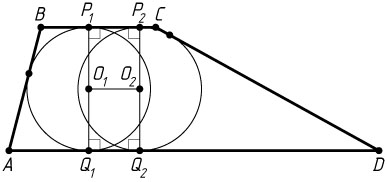
Решение. а) Пусть окружности с центрами O_{1}
и O_{2}
касаются прямой BC
в точках P_{1}
и P_{2}
соответственно, а прямой AD
— в точках Q_{1}
и Q_{2}
соответственно. Тогда точки O_{1}
и O_{2}
— середины противоположных сторон P_{1}Q_{1}
и P_{2}Q_{2}
прямоугольника P_{1}P_{2}Q_{2}Q_{1}
. Значит, O_{1}O_{2}\parallel P_{1}P_{2}
. Следовательно, O_{1}O_{2}\parallel BC\parallel AD
.
б) Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому CO_{2}
и DO_{2}
— биссектрисы углов при боковой стороне CD
трапеции ABCD
.
Пусть прямая CO_{2}
пересекает основание AD
в точке K
. Тогда
\angle CKD=\angle BCK=\angle DCK,
поэтому треугольник CDK
равнобедренный, DC=DK
. Значит, его биссектриса DO_{2}
является высотой и медианой. При этом
AK=AD-DK=AD-CD=39-30=9=BC,
значит, ABCK
— параллелограмм, поэтому CK\parallel AB
и CK=AB=10
.
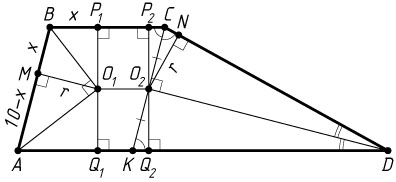
Пусть N
— точка касания с боковой стороной CD
окружности с центром O_{2}
. Тогда O_{2}N
— высота прямоугольного треугольника CO_{2}D
, проведённая из вершины прямого угла. В этом треугольнике известно, что O_{2}C=\frac{1}{2}CK=5
и CD=30
. Значит,
CP_{2}=CN=\frac{O_{2}C^{2}}{CD}=\frac{25}{30}=\frac{5}{6}.
Пусть радиус окружностей равен r
. Тогда
r=O_{2}N=\sqrt{CN\cdot DN}=\sqrt{\frac{5}{6}\cdot\left(30-\frac{5}{6}\right)}=\frac{5\sqrt{35}}{6}.
Пусть M
— точка касания первой окружности со стороной AB
. Обозначим BP_{1}=BM=x
. Тогда AQ_{1}=AM=10-x
. Угол BAD
острый, так как он равен углу CKD
при основании равнобедренного треугольника, поэтому x=BM\lt AM=10-x
, т. е. x\lt5
.
Радиус O_{1}M
— высота прямоугольного треугольника AO_{1}B
, проведённая из вершины прямого угла. Значит, BM\cdot AM=O_{1}M^{2}=r^{2}
, или x(10-x)=\frac{25\cdot35}{36}
. Из этого уравнения и условия x\lt5
находим, что x=\frac{25}{6}
. Следовательно,
O_{1}O_{2}=P_{1}P_{2}=BC-(BP_{1}+CP_{2})=9-\left(\frac{25}{6}+\frac{5}{6}\right)=9-5=4.
Источник: ЕГЭ. — 2018, 1 июня

