10512. На боковых сторонах AB
и AC
равнобедренного треугольника ABC
отложены равные отрезки AP
и CQ
соответственно.
а) Докажите, что средняя линия треугольника, параллельная его основанию, проходит через середину отрезка PQ
.
б) Найдите длину отрезка прямой PQ
, заключённого внутри описанной окружности треугольника ABC
, если AB=AC=BC=3\sqrt{2}
, CQ=AP=\sqrt{2}
.
Ответ. \sqrt{22}
.
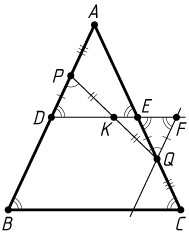
Решение. а) Пусть D
и E
— середины сторон AB
и AC
соответственно. Через точку Q
проведём прямую, параллельную AB
. Пусть эта прямая пересекает прямую DE
в точке F
, а прямые PQ
и DE
пересекаются в точке K
.
Треугольник EQF
равнобедренный, поэтому FQ=QE=DP
. Значит, треугольники QKF
и PKD
равны по стороне и двум прилежащим к ней углам. Следовательно, KQ=KP
, т. е. середина K
отрезка PQ
лежит на средней линии DE
.
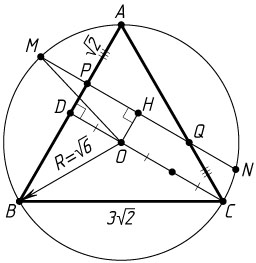
б) Пусть O
— центр окружности радиуса R
, описанной около равностороннего треугольника ABC
, прямая PQ
пересекает эту окружность в точках M
и N
, точка H
— проекция точки O
на хорду MN
. Тогда H
— середина искомого отрезка MN
. Точка D
— середина стороны AB
равностороннего треугольника ABC
, поэтому CD
— высота треугольника ABC
. Тогда
R=\frac{2}{3}CD=\frac{2}{3}\cdot\frac{3\sqrt{2}\cdot\sqrt{3}}{2}=\sqrt{6},
а так как
\frac{AP}{AD}=\frac{\sqrt{2}}{\frac{3}{2}\sqrt{2}}=\frac{2}{3}=\frac{AQ}{AC},
то PQ\parallel CD
. Тогда OHPD
— прямоугольник, значит,
OH=DP=AD-AP=\frac{3}{2}\sqrt{2}-\sqrt{2}=\frac{\sqrt{2}}{2}.
Из прямоугольного треугольника OHM
находим, что
MH=\sqrt{OM^{2}-OH^{2}}=\sqrt{R^{2}-OH^{2}}=\sqrt{6-\frac{1}{2}}=\sqrt{\frac{11}{2}}.
Следовательно,
MN=2MH=2\sqrt{\frac{11}{2}}=\sqrt{22}.
Источник: ЕГЭ. — 2018, 1 июня

