10513. Окружность проходит через вершины A
, B
и C
параллелограмма ABCD
, а также через точки E
и K
, которые лежат на продолжениях сторон AD
и CD
за вершину D
соответственно.
а) Докажите, что BE=BK
.
б) Найдите отношение \frac{AC}{KE}
, если \angle BAD=30^{\circ}
.
Ответ. \frac{1}{\sqrt{3}}
.
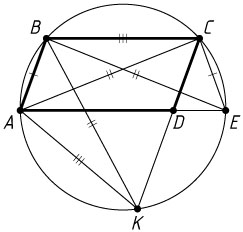
Решение. а) Трапеция ABCE
вписана в окружность, значит, она равнобокая. Диагонали равнобокой трапеции равны, поэтому BE=AC
. Трапеция ABCK
вписана в окружность, значит, она также равнобокая, поэтому AC=BK
. Следовательно, BE=BK
.
б) Треугольники ADC
и KDE
подобны по двум углам, поэтому \frac{AC}{KE}=\frac{AD}{DK}
.
Четырёхугольник ABCK
вписан в окружность, значит,
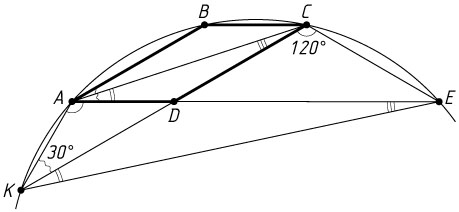
\angle AKD=\angle AKC=180^{\circ}-\angle ABC=\angle BAD=30^{\circ}.
Вписанные углы KAE
и KCE
опираются на одну и ту же дугу, поэтому
\angle KAD=\angle KAE=\angle KCE=\angle BCE-\angle BCD=
=\angle ABC-\angle BAE=150^{\circ}-30^{\circ}=120^{\circ}.
Применив теорему синусов к треугольнику ADK
, получим, что
\frac{AD}{DK}=\frac{\sin\angle AKD}{\sin\angle KAD}=\frac{\sin30^{\circ}}{\sin120^{\circ}}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}.
Примечание. Треугольник KBE
равнобедренный с углом 30^{\circ}
при основании BE
. Пусть BH
— его высота. Тогда
\frac{AC}{KE}=\frac{BK}{KE}=\frac{BK}{2KH}=\frac{1}{2}\cdot\frac{1}{\sin30^{\circ}}=\frac{1}{\sqrt{3}}.
Источник: ЕГЭ. — 2018, 1 июня

