1053. Дан треугольник ABC
, в котором AB=AC
и \angle A=110^{\circ}
. Внутри треугольника взята точка M
, причём \angle MBC=30^{\circ}
, а \angle MCB=25^{\circ}
. Найдите \angle AMC
.
Ответ. 85^{\circ}
.
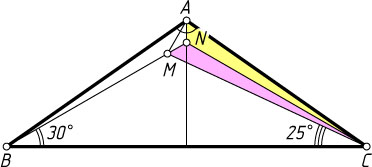
Указание. Пусть N
— точка пересечения прямой BM
с биссектрисой угла BAC
. Докажите, что треугольники ACN
и MCN
равны.
Решение. Пусть N
— точка пересечения прямой BM
с биссектрисой угла BAC
. Поскольку \angle BNC=120^{\circ}
, то
\angle ANC=\angle ANB=120^{\circ},
а так как
\angle ACB=\angle ABC=35^{\circ},~\angle ACN=\angle ABN=5^{\circ},
то
\angle NCM=35^{\circ}-25^{\circ}-5^{\circ}=5^{\circ}.
Поэтому треугольники ACN
и MCN
равны по стороне (CN
— общая) и двум прилежащим к ней углам. Следовательно,
AC=CM,~\angle AMC=\angle MAC=\frac{1}{2}(180^{\circ}-\angle ACM)=\frac{1}{2}(180^{\circ}-10^{\circ})=85^{\circ}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1975, № 2, вариант 2
