1054. Сторона AD
прямоугольника ABCD
в три раза больше стороны AB
. Точки M
и N
делят AD
на три равные части. Найдите \angle AMB+\angle ANB+\angle ADB
.
Ответ. 90^{\circ}
.
Указание. Постройте на большей стороне прямоугольника равный ему другой прямоугольник.
Решение. Первый способ. Предположим, что точка M
расположена между точками A
и N
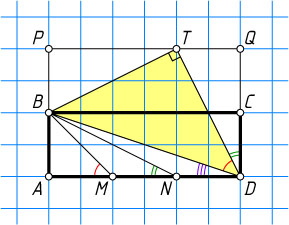
. Рассмотрим прямоугольник BPQC
, равный прямоугольнику ABCD
и имеющий с ним единственную общую сторону BC
.
Пусть T
— точка на стороне PQ
такая, что PT=2TQ
. Тогда прямоугольные треугольники BNA
, TDQ
и BTP
равны по двум катетам. Поэтому
BT=TD,~\angle BTD=180^{\circ}-\angle BTP-\angle QTD=
=180^{\circ}-\angle BTP-(90^{\circ}-\angle QDT)=90^{\circ}.
Следовательно,
\angle BDT=45^{\circ}~\mbox{и}~\angle AMB+\angle ANB+\angle ADB=
=\angle BDT+\angle TDQ+\angle ADB=90^{\circ}.
Второй способ. Поскольку \angle AMB=45^{\circ}
, \tg\angle ANB=\frac{1}{2}
и \tg\angle ADB=\frac{1}{3}
, то
\tg(\angle ANB+\angle ADB)=\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}\cdot\frac{1}{3}}=1.
Следовательно,
\angle ANB+\angle ADB=45^{\circ},~\angle AMB+\angle ANB+\angle ADB=45^{\circ}+45^{\circ}=90^{\circ}.
Источник: Вступительный экзамен в МФТИ. — 1958, билет 20, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 58-20-1, с. 68
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 33, 2.9
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 33, с. 8
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.40, с. 16