10555. Точка M
внутри равностороннего треугольника такова, что \angle BMC=150^{\circ}
. Докажите, что из отрезков, равных MA
, MB
и MC
, можно составить прямоугольный треугольник.
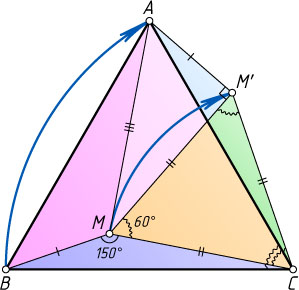
Решение. Рассмотрим поворот относительно точки C
, переводящий вершину B
в A
. Пусть при этом повороте точка A
переходит в A'
, а точка M
— в точку M'
. Тогда отрезок MC
переходит в отрезок M'C
, отрезок MB
— в отрезок M'A
, а треугольник BMC
— в равный ему треугольник AM'C
, поэтому
\angle AM'C=\angle BMC=150^{\circ}.
Треугольник CMM'
равносторонний, поэтому MM'=CM
. Значит,
\angle AM'M=\angle AM'C-\angle MM'C=150^{\circ}-60^{\circ}=90^{\circ}.
Следовательно, прямоугольный треугольник AMM'
составлен из отрезков, равных MA
, MB
и MC
.
Примечание. Верно и обратное: если для внутренней точки M
равностороннего треугольника ABC
верно равенство MA^{2}=MB^{2}+MC^{2}
, то \angle BMC=150^{\circ}
.
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 22.29, с. 206
