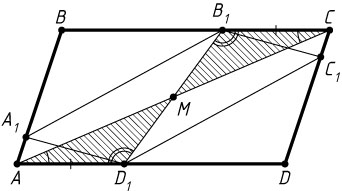
1057. Вершины параллелограмма A_{1}B_{1}C_{1}D_{1}
лежат на сторонах параллелограмма ABCD
(точка A_{1}
лежит на стороне AB
, точка B_{1}
— на стороне BC
и т. д.). Докажите, что центры обоих параллелограммов совпадают.
Указание. Примените признаки равенства треугольников.
Решение. Пусть M
— точка пересечения AC
и B_{1}D_{1}
. Достаточно доказать, что M
— середина AC
и B_{1}D_{1}
.
Из равенства треугольников AA_{1}D_{1}
и CC_{1}B_{1}
(по стороне и двум прилежащим к ней углам) следует равенство отрезков AD_{1}
и CB_{1}
, а из равенства треугольников AMD_{1}
и CMB_{1}
следуют равенства:
AM=MC,~D_{1}M=B_{1}M.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 28, с. 62
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.7, с. 10
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.7, с. 12
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 22
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 160
Источник: Бугаенко В. О. Турниры им. Ломоносова. Конкурсы по математике. — 2-е изд. — М.: ТЕИС, 1995. — № 11, с. 14
