1058. Точка K
— середина стороны AB
квадрата ABCD
, а точка L
делит диагональ AC
в отношении AL:LC=3:1
. Докажите, что угол KLD
прямой.
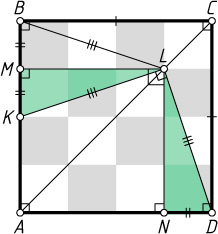
Указание. Пусть M
и N
— проекции точки L
на стороны AB
и AD
. Докажите равенство треугольников KML
и DNL
.
Решение. Первый способ. Пусть M
и N
— проекции точки L
на стороны AB
и AD
. Тогда
KM=MB=ND~\mbox{и}~KL=LB=DL.
Поэтому прямоугольные треугольники KML
и DNL
равны. Следовательно, \angle DLK=\angle NLM=90^{\circ}
.
Второй способ. Поскольку
\overrightarrow{KL}=\overrightarrow{KA}+\overrightarrow{AL}=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}(\overrightarrow{AB}+\overrightarrow{BC})=\frac{1}{4}(\overrightarrow{AB}+3\overrightarrow{BC}),
\overrightarrow{DL}=\overrightarrow{DC}+\overrightarrow{CL}=\overrightarrow{AB}-\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{BC})=\frac{1}{4}(3\overrightarrow{AB}-\overrightarrow{BC}),
то
\overrightarrow{KL}\cdot\overrightarrow{DL}=\frac{1}{16}(3\overrightarrow{AB}^{2}-3\overrightarrow{BC}^{2})=0.
Следовательно, KL
перпендикулярно DL
.
Третий способ. Пусть O
— центр квадрата, H
— середина отрезка OA
. Тогда KH
— средняя линия прямоугольного равнобедренного треугольника AOB
, поэтому KH\parallel BO
, значит, KH\perp LO
. Кроме того,
KH=\frac{1}{2}BO=\frac{1}{4}AC=\frac{1}{2}LH,
а так как
AK=\frac{1}{2}AB=\frac{1}{2}AD,
то прямоугольные треугольники KHO
и KAD
подобны. Следовательно,
\angle ALK=\angle HLK=\angle ADK.
Отрезок AK
виден под одним и тем же углом из точек L
и D
, лежащих по одну сторону от прямой AK
, значит, точки L
, D
, A
и K
лежат на одной окружности, а так как \angle DAK=90^{\circ}
, то DK
— диаметр этой окружности. Следовательно, \angle KLD=90^{\circ}
.
Автор: Богатуров Ю. Т.
Источник: Журнал «Квант». — 1975, № 10, с. 38, М346
Источник: Задачник «Кванта». — М346
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.40, с. 14
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.41, с. 16
