10596. Точка P
, отличная от вершин треугольника ABC
, лежит на описанной окружности этого треугольника. Докажите, что прямые, симметричные прямым PA
, PB
и PC
относительно биссектрис углов соответственно A
, B
и C
, параллельны.
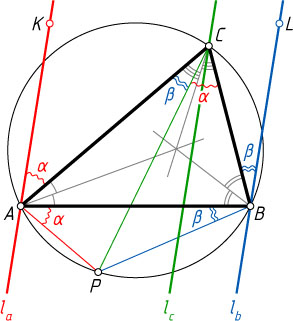
Решение. Рассмотрим случай, изображённый на рисунке. Пусть l_{a}
— прямая, симметричная прямой PA
относительно биссектрисы угла A
, l_{b}
— прямая, симметричная прямой PB
относительно биссектрисы угла B
; K
— точка на прямой l_{a}
, лежащая с точкой B
по разные стороны от прямой AC
, L
— точка на прямой l_{b}
, лежащая с точкой A
по разные стороны от прямой BC
. Обозначим
\angle KAC=\angle PAB=\angle PCB=\alpha,~\angle LBC=\angle PBA=\angle PCA=\beta.
Тогда
\angle KAB+\angle LBA=(\alpha+\angle BAC)+(\beta+\angle ABC)=(\alpha+\beta)+\angle BAC+\angle ABC=
=\angle ACB+\angle BAC+\angle ABC=180^{\circ}.
Следовательно, l_{a}\parallel l_{b}
. Аналогично, l_{a}\parallel l_{c}
, где l_{c}
— прямая, симметричная прямой PC
относительно биссектрисы угла C
.
Аналогично для любого другого случая.
Примечание. 1. См. также статью П.Кожевникова «Изогонально сопряжённые точки», Квант, 2016, N1, с.46-49.
2. См. также статью Д.Прокопенко «Изогональное сопряжение и педальные треугольники», Квант, 2017, N9, с.38-44.
Источник: Прасолов В. В. Точки Брокара и изогональное сопряжение. — М.: МЦНМО, 2012. — с. 5.
Источник: Журнал «Квант». — 2016, № 1, с. 46, упражнение 3
